Vznik kmitania v oscilačnej sústave.
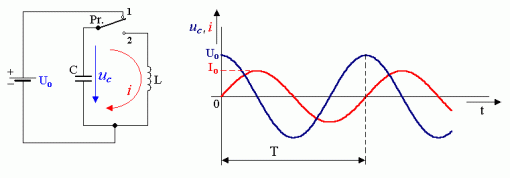
V časti o rozdelení oscilátorov podľa druhu prvku určujúceho frekvenciu vytváraných kmitov sme si spomenuli, že najčastejšie sa používa v oscilátoroch rezonančný obvod a to buď sériový alebo paralelný. Všimnime si teda, aké fyzikálne deje prebiehajú v obvode paralelného rezonančného obvodu použitého v oscilačnej sústave. Pre jednoduchosť uvažujme najprv použitie ideálneho ( bezstratového ) kondenzátora C a ideálnej ( bezstratovej ) cievky L. Obvod nech je zapojený podľa obrázka.

Proces sledovania si rozdelíme na dva hlavné kroky v závislosti od polohy prepínača
Pr.Tým došlo k premene energie elektrického poľa kondenzátora WC na energiu magnetického poľa cievky WL. Ďalej sa bude prúd v obvode zmenšovať a tým aj energia magnetického poľa. Pritom sa bude v cievke indukovať podľa Lenzovho zákona napätie takej polarity, že bude spomaľovať zmenšovanie prúdu. Toto napätie, ako z Lenzovho zákona vyplýva, má opačnú polaritu ako napätie Uo, ktoré prúd i v obvode vyvolalo. Kondenzátor C sa začne nabíjať na toto napätie až sa nabije na maximálnu hodnotu tohoto záporného napätia, t.j. uC = – Uo. V okamihu, keď je uC = – Uo je prúd i v obvode nulový ( i = 0 A ). Tým došlo k premene energie magnetického poľa cievky WL na energiu elektrického poľa kondenzátora WC. Táto vzájomná zmena energií sa periodicky opakuje. Charakter zmien napätia uC a prúdu i v obvode je znázornený na obrázku hore. Časový priebeh takto vytváraných kmitov predstavuje striedavé napätie a prúd, ktoré vieme popísať rovnicami :
Tento jav však nastáva len vtedy, keď sa c
elá energie WC premení na energiu WL a naopak, teda ak rezonančný obvod LC nemá odpor, na ktorom by sa časť energie premieňala na teplo. Len za tohto predpokladu môžu vzniknúť periodicky sa opakujúce netlmené harmonické kmity napätia a prúdu s konštantnou amplitúdou. Súčasne vidieť, že prúd v obvode sa oneskoruje za napätím o 90°. Frekvenciu kmitov určíme z rovnosti energií WC = WL , teda :Pre napätie Uo platí :
takže po dosadení do rovnice ( 1 ) dostávame :
po vykrátení a úprave dostávame známy Thomsonov vzťah :
Z rovnosti energií tiež vyplýva, po úprave rovnice ( 1 ), že :
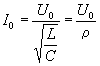 kde
kde je vlnový odpor rezonančného obvodu pre rezonančnú frekvenciu fo.
Doposiaľ sme sa zaoberali rezonančným obvodom tvoreným ideálnym kondenzátorom a ideálnou cievkou. V praxi však ideálne prvky neexistujú a či kondenzátor alebo cievka majú určité reálne stratové odpory. Pretože stratový odpor cievky je omnoho väčší ako stratový odpor kondenzátora, pri sledovaní vlastností reálneho rezonančného obvodu RLC stratový odpor kondenzátora zanedbáme. Obvod nech je zapojený podľa obrázka.
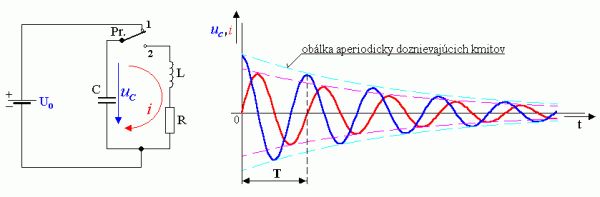
Ako z obrázka vidno stratový rezistor R je zapojený v sérii s cievkou L
. Podobne ako sme si vysvetlili vyššie, aj tu dochádza k premene energie elektrického poľa kondenzátora WC na energiu magnetického poľa cievky WL, ale aj na tepelnú energiu WR na stratovom rezistore R , ktorá sa vyžiari do okolitého prostredia. Tým amplitúda vzniknutých kmitov postupne klesá, až kmity úplne zaniknú. Hovoríme o aperiodicky doznievajúcich kmitoch.. Charakter zmien napätia uC a prúdu i v obvode je znázornený na obrázku hore.Všeobecne sa môžu pomery v tomto obvode opísať diferenciálnou rovnicou, z ktorej sa môže vyjadriť frekvencia kmitania podľa výrazu :
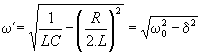 ( 2 )
( 2 )
pričom
d predstavuje činiteľ tlmenia a udáva rýchlosť poklesu amplitúdy kmitov:![]()
Činiteľ tlmenia úzko súvisí s kvalitou
Q rezonančného obvodu. Kvalita obvodu je určená vzťahom :![]()
Čím je väčšie tlmenie obvodu, tým je menšia jeho kvalita a naopak
.Pre malé hodnoty odporu stratového rezistora R
môžeme v rovnici ( 2 ) člen d zanedbať a tým sa frekvencia tlmených kmitov w´ sústavy so stratovým rezistorom R bude rovnať frekvencii kmitov wo sústavy bez stratového rezistora R. Časový priebeh vytváraných tlmených kmitov predstavuje striedavé napätie a prúd, ktoré vieme popísať rovnicami :uC = Uo.e-
d.t.cos wt a i = Io.e-d.t.sin wtAby rezonančný obvod kmital s konštantnou amplitúdou, treba sústavne v každom časovom okamihu kompenzovať účinky strát na rezistore
R. Vhodným prepojením rezonančného obvodu a aktívneho prvku, najčastejšie zosilňovača, môžeme zostrojiť oscilátor, ktorý vytvára netlmené kmity. Zosilňovač, ako aktívny štvorpól kompenzuje straty v rezonančnom obvode.| Všeobecné podmienky kmitania |