V priebehu periodických signálov sa vyskytujú určité zákonitosti, na základe ktorých sa Fourierov rozvoj anulovaním niektorých členov zjednoduší. Tvar krivky signálu nám umožňuje posúdiť, či je možné zjednodušenie. Pre pochopenie postupov pri zjednodušovaní nám poslúžia obrázky a) až d). Postupujeme podľa nasledovných pravidiel :

a)	Ak je priebeh krivky súmerný podľa začiatku [ obrázok a )],  t.j. ak platí F(-t)= -F(t) ( nepárna funkcia ), výpočtom zistíme, že všetky činitele Fourierovho rozvoja pri kosínusových zložkách sú nulové. Teda : F(t) = b1. sinwot + b2. sin 2wot + ... + bn. sin nwot
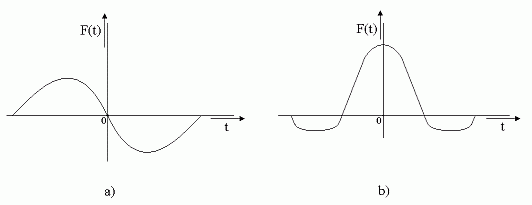b)	Ak je krivka súmerná podľa osi y [ obrázok b )],  t.j. ak platí F(-t)= F(t) ( párna funkcia ), obsahuje Fourierov rozvoj len kosínusové zložky. Teda : F(t) = a0 + a1. coswot + a2. cos 2wot + ... + an. cos nwot
c)	Ak sa opakujú hodnoty priebehu z prvej polovice periódy v druhej polovici s opačným znamienkom [obrázok c) ] , t.j. ak platí 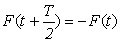,  potom obsahuje Fourierov rozvoj len nepárne členy : F(t) = A1. cos (wot - j1 ) + A3. cos (3wot - j3 )+ ....
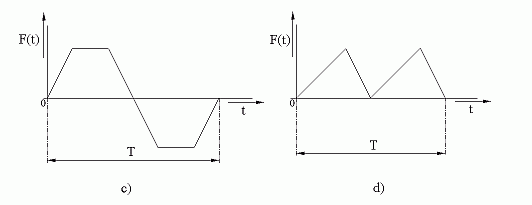d)	Ak sa opakujú hodnoty funkcie v druhej polovici periódy s rovnakým znamienkom [ obrázok d) ], t.j. ak platí 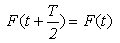,  potom obsahuje Fourierov rozvoj len párne členy : F(t) = A0 + A2. cos (2wot - j2 ) + A4. cos (4wot - j4 )+ ....

       Úlohou harmonickej analýzy je určiť pre danú funkciu F(t) hodnoty činiteľov  a_n,  b_n,  alebo amplitúdy  A_n  a fázové posuny  j_n  jednotlivých harmonických. Na tento účel sa používajú štyri základné metódy :

• matematická
• výpočtová
• grafická
• elektronická

       Týmito metódami sa bližšie nebudeme zaoberať, pretože metódy matematická, výpočtová a grafická sa najviac využívajú pri používaní počítača na realizáciu harmonickej analýzy. Tu počítač vykonáva časovo náročnú a rutinnú činnosť namiesto človeka. Využívajú sa hlavne v oblasti teoretického výskumu. Elektronická metóda sa používa v technickej praxi pri oživovaní a nastavovaní elektronických zariadení, najmä vo vysokofrekvenčnej elektrotechnike. Pre tieto účely slúžia špeciálne zariadenia určené na analýzu sledovaného signálu nazývané spektrálne analyzátory, alebo jednoduchšie zariadenia selektívne milivoltmetre.