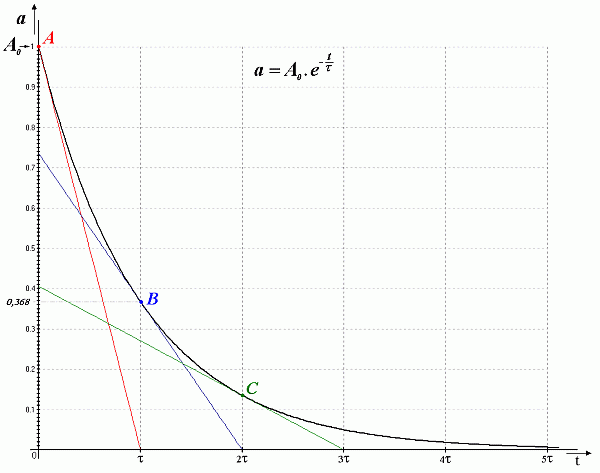
Graficky časovú konštantu môžeme definovať takto : Vzdialenosť ( v smere časovej osi ) dotykového bodu dotyčnice s exponenciálou a priesečníka dotyčnice s časovou osou sa rovná časovej konštante  t ,  bez ohľadu na polohu dotykového bodu. Túto skutočnosť ilustruje obrázok - vzdialenosť bodov A a B, B a C, v smere časovej osi  t , je vždy rovná časovej konštante  t.   Táto skutočnosť platí aj pre situáciu nárastu exponenciály, napr. pri nabíjaní kondenzátora.

       Časovú konštantu môžeme definovať slovne aj z dotyčnice k exponenciále v čase  t = 0 s  ( kreslená červenou farbou ), z ktorej je možné odvodiť, že časová konštanta odpovedá dobe, za ktorú by prechodný dej poklesu obvodovej veličiny z maximálnej na nulovú hodnotu skončil, keby prebiehal lineárne ( konštantnou rýchlosťou.)  To platí aj pre prechodný dej nárastu obvodovej veličiny z nulovej na maximálnu hodnotu.

       Časovú konštantu číselne môžeme definovať tak, že je to čas, za ktorý klesne veľkosť obvodovej veličiny na hodnotu 0,368 z jej maximálnej hodnoty ( pri náraste vzrastie na hodnotu 0,632 jej maximálnej hodnoty.)