 |
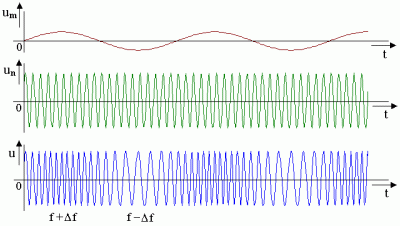
modulačný signál |
| nosný signál ( nosná vlna ) | |
| modulovaný nosný signál |
Pri frekvenčnej modulácii sa mení frekvencia nosnej vlny v rytme modulačného signálu. Amplitúda modulovanej vlny ostáva konštantná.
Pri frekvenčnej modulácii rozlišujeme tieto pojmy :
| - | kmitočet modulačného signálu W = 2.p.F |
| - | kmitočet nosnej vlny w = 2.p.f |
| - | Odchýlka Dw = 2.p.Df nazývaná frekvenčný zdvih ( deviacia ). Ide o maximálnu zmenu kmitočtu nosnej vlny w udávanú v Hz. Tento frekvenčný zdvih nezávisí od frekvencie modulačného signálu W , ale závisí od jeho amplitúdy Um ( je to jedna z podmienok pre neskreslenú moduláciu FM.), čo môžeme vyjadriť vzťahom :
Frekvencia modulačného signálu W určuje koľkokrát za sekundu sa zmení kmitočet nosnej vlny z w - Dw na w + Dw a naopak, ako to vidno na obrázku. |
 |
modulačný signál |
| nosný signál ( nosná vlna ) | |
| modulovaný nosný signál |
| um = Um.sinWt | ( 1 ) ....... | modulačný signál s amplitúdou Um a kmitočtom W |
| un = Un.sinwt | ( 2 ) ....... | nosný signál s amplitúdou Un a kmitočtom w |
| u = Un.sinw'(t) | ( 3 ) ....... | nosný modulovaný signál s pôvodnou amplitúdou Un , ale s kmitočtom w'(t), ktorý sa s časom mení v rytme modulačného signálu um. Túto skutočnosť vieme zapísať vzťahom :
|
Môžeme teda povedať, že zmena kmitočtu nosnej vlny tak obsahuje obidve charakteristické znaky prenášaného nf signálu a to jeho amplitúdu Um a kmitočet W.
Poznámka!
V rovnici ( 4 ) sa použil cosinus preto, lebo ak by sme frekvenčne modulovaný signál zakreslili vektorovo zistili by sme, že vektory postranných frekvencií w + W sú oproti nosnému kmitočtu w otočené o ± 90°.
Pretože uhlový kmitočet je časovou deriváciou fázy, dostaneme vyjadrenie kmitočtu w'(t) frekvenčne modulovanej nosnej vlny integráciou rovnice ( 4 ) podľa času :
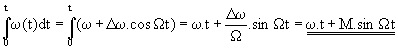 ( 5 )
( 5 )Po dosadení výsledku rovnice ( 5 ) do rovnice ( 3 ) dostávame výslednú rovnicu pre frekvenčne modulovanú nosnú vlnu :
Túto rovnicu môžeme rozvinúť do nekonečného radu jednoduchých výrazov určenými Besselovými funkciami takto :
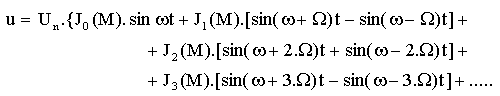
Rovnica ukazuje, že frekvenčne modulovaná nosná vlna obsahuje pôvodnú nosnú vlnu s kmitočtom w a nekonečný počet párov postranných frekvenčných zložiek, daný súčtom a rozdielom kmitočtu nosnej vlny w a všetkých harmonických násobkov kmitočtu modulačného signálu W. Vzdialenosť jednotlivých zložiek je rovný frekvencii F modulačného signálu. Amplitúdy postranných zložiek sú určené Besselovými funkciami J0(M), J1(M), J2(M), .... Jn(M) nultého až n-tého rádu argumentu M. Hodnoty týchto funkcií nájdeme v matematických tabuľkách.
V praxi sa ukázalo, že na prenos informácie s dostatočne malým skreslením postačí preniesť všetky postranné zložky, ktorých amplitúda je väčšia ako 1 % amplitúdy nosného nemodulovaného signálu. Na výpočet potrebnej šírky prenášaného frekvenčného pásma, potrebného na splnenie tejto požiadavky, môžeme použiť nasledujúci vzťah :
V závislosti od hodnoty činiteľa frekvenčnej modulácie M rozlišujeme dva typy frekvenčnej modulácie. Ak M < 1 ide o úzkopásmovú FM a ak M > 1 ide o širokopásmovú FM. Ako príklad širokopásmovej FM môžem uviesť rozhlasové vysielanie, kde sa používa frekvenčný zdvih Df = 50 kHz ( poprípade 75 kHz ) a maximálny modulačný kmitočet F = 15 kHz. Ako príklad úzkopásmovej FM môže poslúžiť frekvenčný zdvih Df = 15 kHz používaný v mobilných vysielačoch pracujúcich na vlnách kratších ako 10 m.
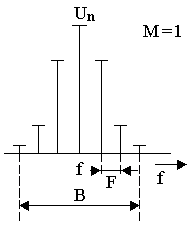
S hodnotou činiteľa M súvisí dôležitý kvalitatívny ukazovateľ prenosu správ určujúci jeho akosť a to pomer amplitúdy signálu k amplitúde šumu - S/N. Platí, že čím je M väčšie, tým väčší je pomer signál/šum. Na druhej strane však platí, že s narastajúcim M narastá, pre kvalitný prenos, aj potrebná šírka frekvenčného pásma ako to vidno na obrázkoch nižšie. Nedodržanie potrebnej šírky pásma, jej zmenšenie, vedie ku zhoršeniu pomeru signál/šum a hlavne ku zvýšeniu skreslenia výstupného signálu na vyšších dynamických úrovniach. ( napr. údery do bubna v tanečnej hudbe, atď.)
 |
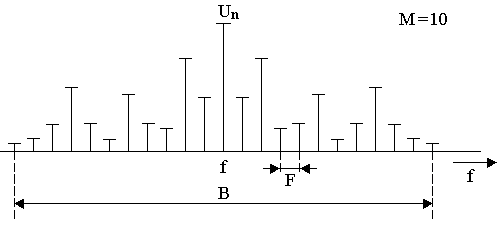 |
FM pre M = 1 |
Na záver zhrnieme výhody frekvenčnej modulácie v porovnaní s amplitúdovou moduláciou :
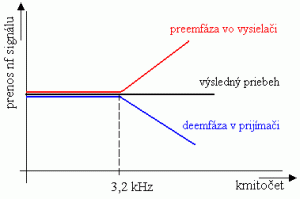 Poznámka : Z hľadiska energetického, napríklad v hudbe, sú frekvencie stredné a vysoké zastúpené len asi z 20 %. Zvyšná energia je sústredená v nízkych frekvenciách - basoch. Naopak šum má svoju prevažnú časť energie sústredenú v zložkách s vyššími frekvenciami. Najväčším zdrojom šumu v prenosovej ceste sú vstupné obvody, zmiešavač a frekvenčný demodulátor na strane prijímača. Z povedaného vyplýva, že pri prenose zložiek s vyššími frekvenciami, by po demodulácii výrazne klesol odstup signál/šum. Ak však na strane vysielača preemfázou umelo zvýšime energetickú úroveň zložiek s vyššími frekvenciami na strane prijímača, za demodulátorom, dostávame priaznivý pomer signál/šum. Použitím deemfázy obmedzíme prenos signálov s vyššími frekvenciami, teda aj zložiek šumu z demodulátora.
Poznámka : Z hľadiska energetického, napríklad v hudbe, sú frekvencie stredné a vysoké zastúpené len asi z 20 %. Zvyšná energia je sústredená v nízkych frekvenciách - basoch. Naopak šum má svoju prevažnú časť energie sústredenú v zložkách s vyššími frekvenciami. Najväčším zdrojom šumu v prenosovej ceste sú vstupné obvody, zmiešavač a frekvenčný demodulátor na strane prijímača. Z povedaného vyplýva, že pri prenose zložiek s vyššími frekvenciami, by po demodulácii výrazne klesol odstup signál/šum. Ak však na strane vysielača preemfázou umelo zvýšime energetickú úroveň zložiek s vyššími frekvenciami na strane prijímača, za demodulátorom, dostávame priaznivý pomer signál/šum. Použitím deemfázy obmedzíme prenos signálov s vyššími frekvenciami, teda aj zložiek šumu z demodulátora.
Nevýhody: