), ktorá má v intervale T konečný počet extrémov a nespojitostí, možno vyjadriť nekonečným goniometrickým radom v tvare :Matematická podstata harmonickej analýzy a podmienky, v ktorých ju možno realizovať, sú vyjadrené Fourierovou vetou :
Každú jednoznačne určenú periodickú funkciu F(t) ( s opakovacou periódou T a opakovacou frekvenciou ), ktorá má v intervale T konečný počet extrémov a nespojitostí, možno vyjadriť nekonečným goniometrickým radom v tvare :
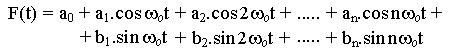
Pravá strana rovnice sa nazýva Fourirovým radom ( rozvojom.)
| a0 | ..... | predstavuje strednú hodnotu funkcie F(t) za čas T a nazýva sa jednosmerná zložka | ||
| cos nwt | ..... | sú kosínusové zložky |  |
|
| Fourierového rozvoja. n ... je celé kladné číslo. | ||||
| sin nwt | .... | sú sínusové zložky | ||
| an, bn | .... | sú činitele ( koeficienty ) Fourierového radu. | ||
Pre ilustráciu daných tvrdení nám poslúži nasledujúci obrázok, na ktorom je znázornená analýza, poprípade syntéza signálu pílovitého priebehu pre sedem harmonických zložiek.
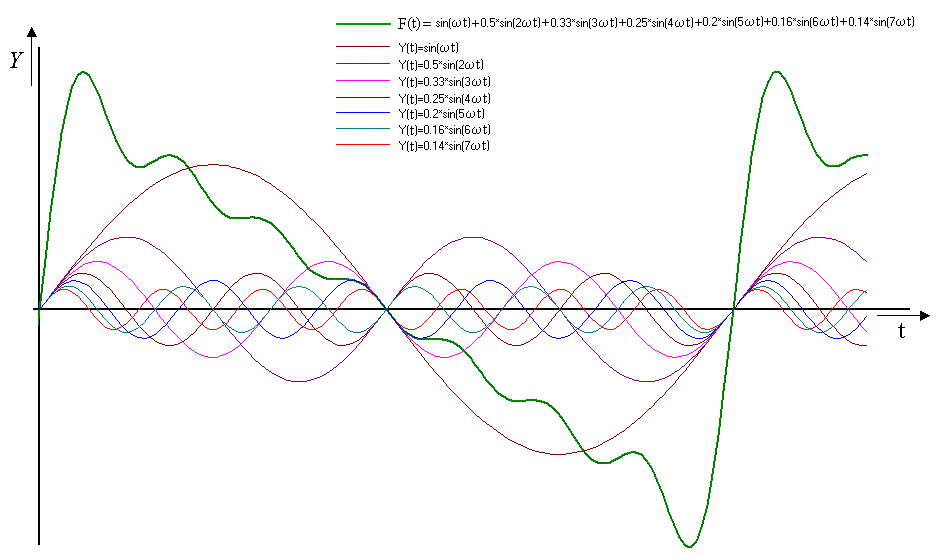
Ak si lepšie všimneme Fourierov rozvoj funkcie F(t), môžeme zistiť, že kosínusové aj sínusové zložky obsahujú členy s rovnakou frekvenciou w0 , 2w0 , 3w0 , ... nw0 . Potom podľa známej goniometrickej poučky môžeme každú takúto dvojicu členov vyjadriť jediným členom.
Pre prvú harmonickú ( základnú ) bude mať tento člen tvar :
Potom Fourierov rozvoj môžeme napísať aj v tvare :
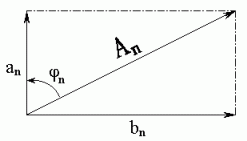
A platí :
 |
 |
 |
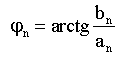| an = An.cos wn | bn = An.sin wn |
S Fourierovým rozvojom úzko súvisí frekvenčné spektrum signálu.