f)   Stabilita zosilňovača so zápornou spätnou väzbou


  Nedostatkom zosilňovača so spätnou väzbou je možnosť vzniku parazitných kmitov na výstupe a to aj v tom prípade, keď na vstupe nepôsobí žiadny signál. Ako sme už spomenuli pri odvodzovaní vplyvu zápornej spätnej väzby na napäťové zosilnenie, prenos bloku zosilnenia A a prenos bloku spätnej väzby ß sú vo všeobecnosti komplexné čísla. Teda:

A = |A|.     ß = |ß|.
a ich súčin:
A.ß = |A|.|ß|

  Pri splnení podmienky jA + jß = 2.k.p (k = 0,1,2,-) platí, že A.ß = |A|.|ß| a ide teda o kladnú spätnú väzbu. Ak sa splní ešte aj podmienka, že súčin A.ß > 1,  vznikajú v obvode zosilňovača samočinné kmity, oscilácie.

  Lepšiu predstavu o stabilite zosilňovača so spätnou väzbou dostaneme, ak ho chápeme ako regulovanú sústavu. Stabilitu regulovaných sústav určujeme podľa viacerých kritérií ( imitančné, Hurwitzovo, Nyquistovo ). Najznámejšie je Nyquistovo kritérium stability, pretože umožňuje nielen kvalitatívne, ale aj kvantitatívne posúdenie stability zosilňovača.

  Nyquistovo kritérium stability je nasledovné:
Ak zavedieme do uzavretého obvodu zosilňovač - spätná väzba malý impulzný signál a sledujeme charakter jeho zmien, sú možné dva prípady:
  - signál pri viacnásobnom prechode cez zosilňovač sa s časom utlmuje - sústava je stabilná
  - signál pri viacnásobnom prechode cez zosilňovač s časom narastá - sústava je nestabilná

  Ďalšou skutočnosťou, ktorá prispieva k nestabilite zosilňovača so zápornou spätnou väzbou ako celku je aj to, že prenos A bloku zosilnenia a prenos ß bloku spätnej väzby sú frekvenčne závislé ( tieto bloky obsahujú reaktančné prvky, kapacity a indukčnosti ). Súčin A.ß môžeme vyjadriť v komplexnom zložkovom tvare:

A.ß = a(f) + j.b(f)

  Dosadením rôznych frekvencií od 0 do môžeme určiť pre každú frekvenciu zložky a(f) a b(f) a vyniesť ich do grafu v Gaussovej rovine. Modul |A.ß| a argument j pre danú frekvenciu dostaneme z nasledujúcich rovníc:

Spojením koncových bodov fázora |A.ß| pre frekvencie od 0 do , dostaneme krivku stability.

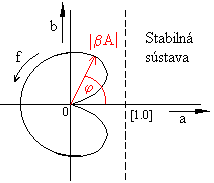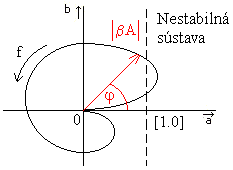Frekvenčná charakteristika stabilnej sústavyFrekvenčná charakteristika nestabilnej sústavy

Bod [1,0] je bod stability a platí:
  ak všetky body frekvenčnej charakteristiky sústavy ležia vľavo od bodu [1,0], hovoríme o stabilnej sústave
  ak aspoň jeden bod frekvenčnej charakteristiky sústavy leží vpravo od bodu [1,0], hovoríme o nestabilnej sústave.

  Z hore uvedeného rozboru vyplýva, že zavedením zápornej spätnej väzby do obvodu zosilňovača sa jeho stabilita ako celku zhorší.
!!!   Použitie obsahu stránok alebo ich častí na "kvaziautorské" a komerčné účely je v rozpore s autorskými právami a je možné len so súhlasom autora   !!!
Spracoval :  Ing. Alexander Žatkovič
Prípadné pripomienky alebo otázky zasielajte na adresu